
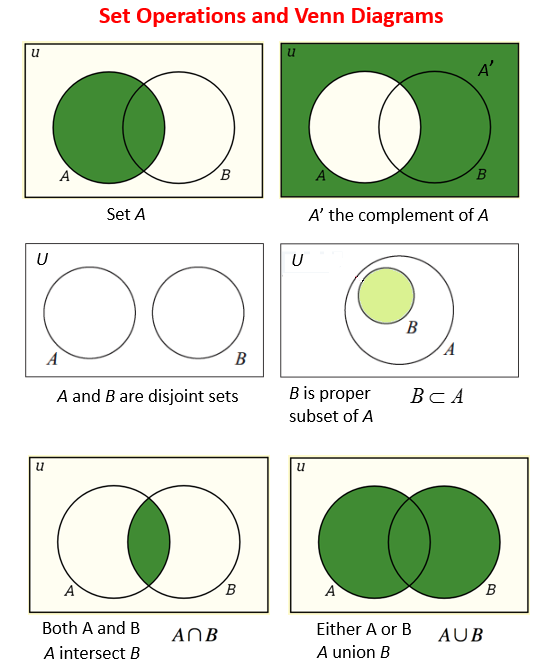

How do you use Venn diagrams to solve set operations?Īns: In a Venn diagram, the universal set is represented by a quadrilateral, usually a rectangle. Learn About Representation of Sets Frequently Asked Questions (FAQs) While the first three operations are performed on two or more sets, the fourth operation is usually performed on a single set or a resulting set of the first three operations. The four main operations performed using Venn diagrams are – intersection, union, difference, and complement. It also explains how Venn diagrams were first used and the steps to draw one. This article covers the various operations performed on sets using Venn diagrams after explaining the definition and examples for sets in mathematics. If each person chose at least one of the beverages, how many people dined at the buffet?Īns: \(n\left( \) \(25\) people chose both coffee and juice. At a breakfast buffet, \(93\) people chose to have coffee, and \(47\) people chose juice. The intersection of two sets is denoted as \(A \cap B\). In a Venn diagram, this is represented in the overlapping region of the two circles. The intersection of sets is nothing but elements that are common to sets \(A\) and \(B\). Let us now try to combine the concept of Venn diagrams and operations using two sets, \(A\) and \(B\). Operationĭenotes elements that are in set \(A\) but not in set \(B\) Operations on Setsįour basic operations are carried out on sets. Highlights data patterns that may not be visible otherwise. It helps reason complex issues using logic.ĥ. It helps students visualize the relationships between different sets.Ĥ. A Venn diagram can be used for both comparison and classification.ģ. The elements that are members of more than one set are written in the overlapping area.Ī simple Venn diagram of two overlapping sets, \(A\) and \(B\), will appear as shown below.ġ. The elements of each set are written in the corresponding circles.ĥ. Each circle is labelled with the name of the set to help in identification.Ĥ. For ease of use, it is generally restricted to \(3\) circles or subsets.ģ. Every set to be drawn will be a subset of the universal set. The overlapping region will contain the elements that are members of all the overlapping sets. The outside of the circle represents the elements that are not members of the set. The inside of each circle represents the elements that are members of a set. Circles are usually preferred as it is easy to draw overlapping circles. Any closed figure can be used in place of the circle. They usually consist of overlapping circles. Drawing a Venn DiagramĪ Venn diagram is drawn using simple curves and lines on a plane. People who are tall for me may not be considered tall for someone who is \(6\) feet tall themselves. For example, I cannot make a set with tall people. Also, this rule must be universal and not subjective. Observe that the only condition for the elements to be in a set is that they must all be connected by the same rule of law. The elements in a universal set are not repeated. A universal set is a set that has all the elements of all the related sets. As it is impossible to list all the elements in an infinite set, a formula usually represents it.Ĥ. A set may have an infinite number of elements. A set with only one element is called a singleton set.ģ. A set with no elements is called an empty set or a null set. For example, for a set \(A\), cardinality is written as \(\left| A \right|\). Cardinality is represented by vertical bars. It represents the number of elements in a set. Cardinality of a set is the measure of the size of a set.


 0 kommentar(er)
0 kommentar(er)
